Проекция предмета на одну плоскость
 Разобравшись с проецированием точки, можно построить чертеж любого предмета или детали, либо перейти к решению простых задач по начертательной геометрии.
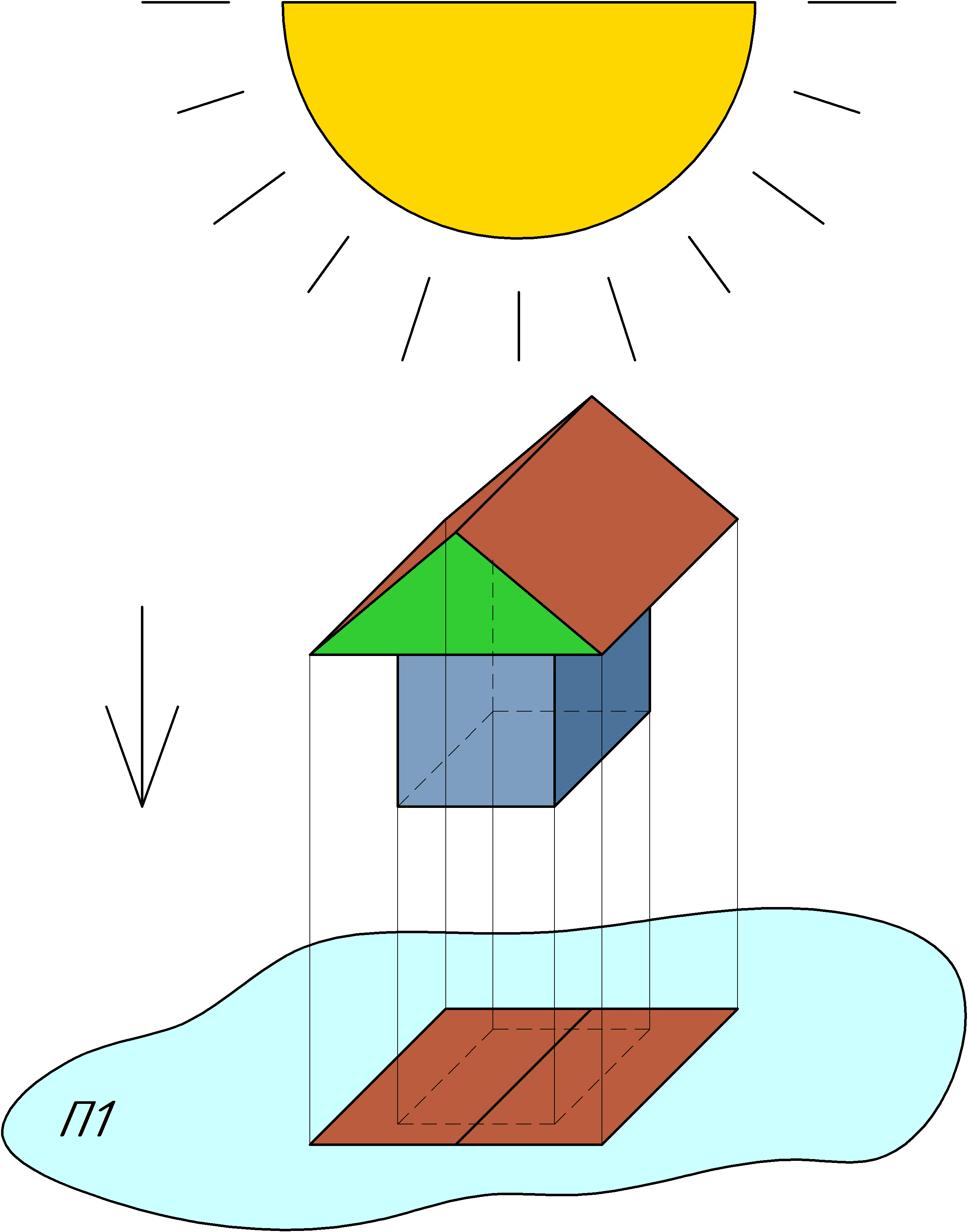
Рассмотрим пояснительный пример отображения предмета на некоторой воображаемой ровной и плоской поверхности, после чего перейдем к построению двух проекций точки онлайн. В качестве предмета возьмем небольшое здание с крышей и стенами,
которое показано на рисунке. Изобразим его чертеж на поверхности. Удобнее всего поверхность совместить с землей, а источник освещения выбрать вертикально сверху, как импровизированное солнце,
которое светит прямо вертикально. В результате на земле получится тень от крыши. Кроме крыши можно увидеть изображение стен, только они показаны штриховыми линиями, так как расположены ниже и
тень от крыши их закрывает. Кроме всего прочего, можно увидеть на крыше еще и перелом в виде линии. В результате мы имеем некоторый упрощенный чертеж домика на одной поверхности.
Воспроизвести его или построить вживую по имеющемуся чертежу невозможно, так как нет информации о высоте крыши, стен, наличии окон, дверей и прочих деталей. Для этих целей требуется выполнить
еще несколько изображений/чертежей либо разрезов. Использование одной плоскости малоинформативно в данном случае, однако такой метод довольно широко применяется в геологии, чертежах географических карт и т.д.
Разобравшись с проецированием точки, можно построить чертеж любого предмета или детали, либо перейти к решению простых задач по начертательной геометрии.
Рассмотрим пояснительный пример отображения предмета на некоторой воображаемой ровной и плоской поверхности, после чего перейдем к построению двух проекций точки онлайн. В качестве предмета возьмем небольшое здание с крышей и стенами,
которое показано на рисунке. Изобразим его чертеж на поверхности. Удобнее всего поверхность совместить с землей, а источник освещения выбрать вертикально сверху, как импровизированное солнце,
которое светит прямо вертикально. В результате на земле получится тень от крыши. Кроме крыши можно увидеть изображение стен, только они показаны штриховыми линиями, так как расположены ниже и
тень от крыши их закрывает. Кроме всего прочего, можно увидеть на крыше еще и перелом в виде линии. В результате мы имеем некоторый упрощенный чертеж домика на одной поверхности.
Воспроизвести его или построить вживую по имеющемуся чертежу невозможно, так как нет информации о высоте крыши, стен, наличии окон, дверей и прочих деталей. Для этих целей требуется выполнить
еще несколько изображений/чертежей либо разрезов. Использование одной плоскости малоинформативно в данном случае, однако такой метод довольно широко применяется в геологии, чертежах географических карт и т.д.
Проекция точки на П0
 При создании карт используется метод проецирования на одну поверхность, его еще называют методом с числовыми отметками. Суть заключается в том, что имеется некоторая поверхность,
П0 и точки, которые располагаются выше ее, имеют положительный индекс, в котором записано расстояние от этой точки и до плоскости в метрах. Те, которые располагаются ниже,
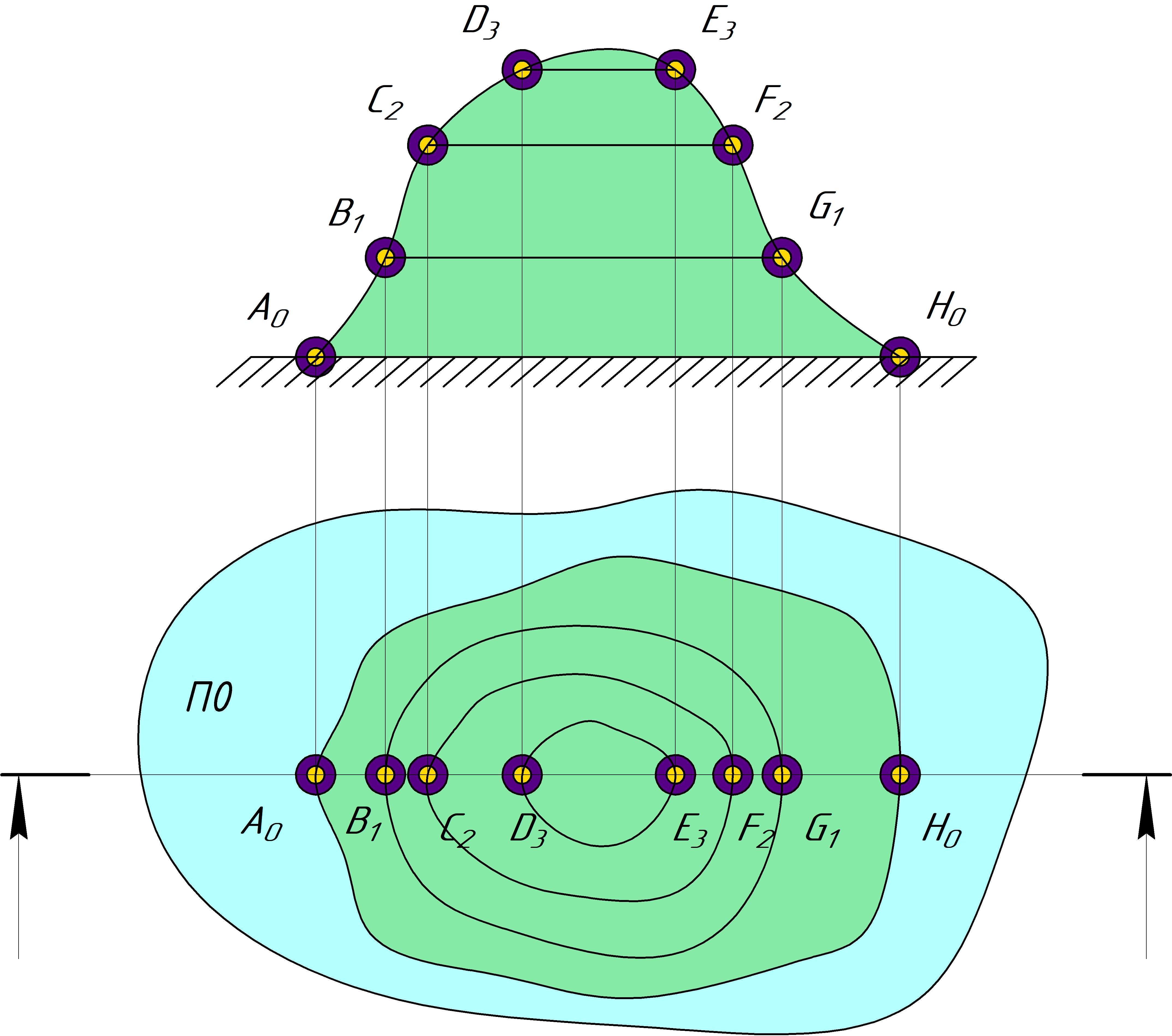
имеют отрицательный индекс. Множество точек с одинаковыми отметками образуют кривые линии, горизонтали. На рисунке снизу показан чертеж холма в виде горизонталей, на нем указаны точки
ABCDEFGH, каждая из которых принадлежит своей горизонтали. К примеру, точки А и H принадлежат горизонтали с "высотой" в 0м, B и G - в 1м, С и F - в 2м, D и E - в 3м. Как было описано выше,
чертеж, который показан снизу, дает некоторое упрощенное изображение. Благодаря отметкам, можно понять что это небольшой холм высотой чуть больше 3м. Для более детального изображения
используются разрезы. В данном случае показан разрез фронтальной плоскостью, стрелочками показан вид, а сверху на рисунке указан чертеж холма в срезе. Имея точки, которые были проставлены
в местах пересечения линии разреза и горизонталей, можно получить чертеж разреза некоторого элемента с разных сторон, достаточно лишь на продолжении линий расставить точки в соответствии с
их высотой, после чего соединить плавной линией. Приравняв данный разрез к трапециям или треугольникам, можно вычислить площадь холма и в дальнейшем определить объем земляных работ.
При создании карт используется метод проецирования на одну поверхность, его еще называют методом с числовыми отметками. Суть заключается в том, что имеется некоторая поверхность,
П0 и точки, которые располагаются выше ее, имеют положительный индекс, в котором записано расстояние от этой точки и до плоскости в метрах. Те, которые располагаются ниже,
имеют отрицательный индекс. Множество точек с одинаковыми отметками образуют кривые линии, горизонтали. На рисунке снизу показан чертеж холма в виде горизонталей, на нем указаны точки
ABCDEFGH, каждая из которых принадлежит своей горизонтали. К примеру, точки А и H принадлежат горизонтали с "высотой" в 0м, B и G - в 1м, С и F - в 2м, D и E - в 3м. Как было описано выше,
чертеж, который показан снизу, дает некоторое упрощенное изображение. Благодаря отметкам, можно понять что это небольшой холм высотой чуть больше 3м. Для более детального изображения
используются разрезы. В данном случае показан разрез фронтальной плоскостью, стрелочками показан вид, а сверху на рисунке указан чертеж холма в срезе. Имея точки, которые были проставлены
в местах пересечения линии разреза и горизонталей, можно получить чертеж разреза некоторого элемента с разных сторон, достаточно лишь на продолжении линий расставить точки в соответствии с
их высотой, после чего соединить плавной линией. Приравняв данный разрез к трапециям или треугольникам, можно вычислить площадь холма и в дальнейшем определить объем земляных работ.
Проекция предмета на две плоскости
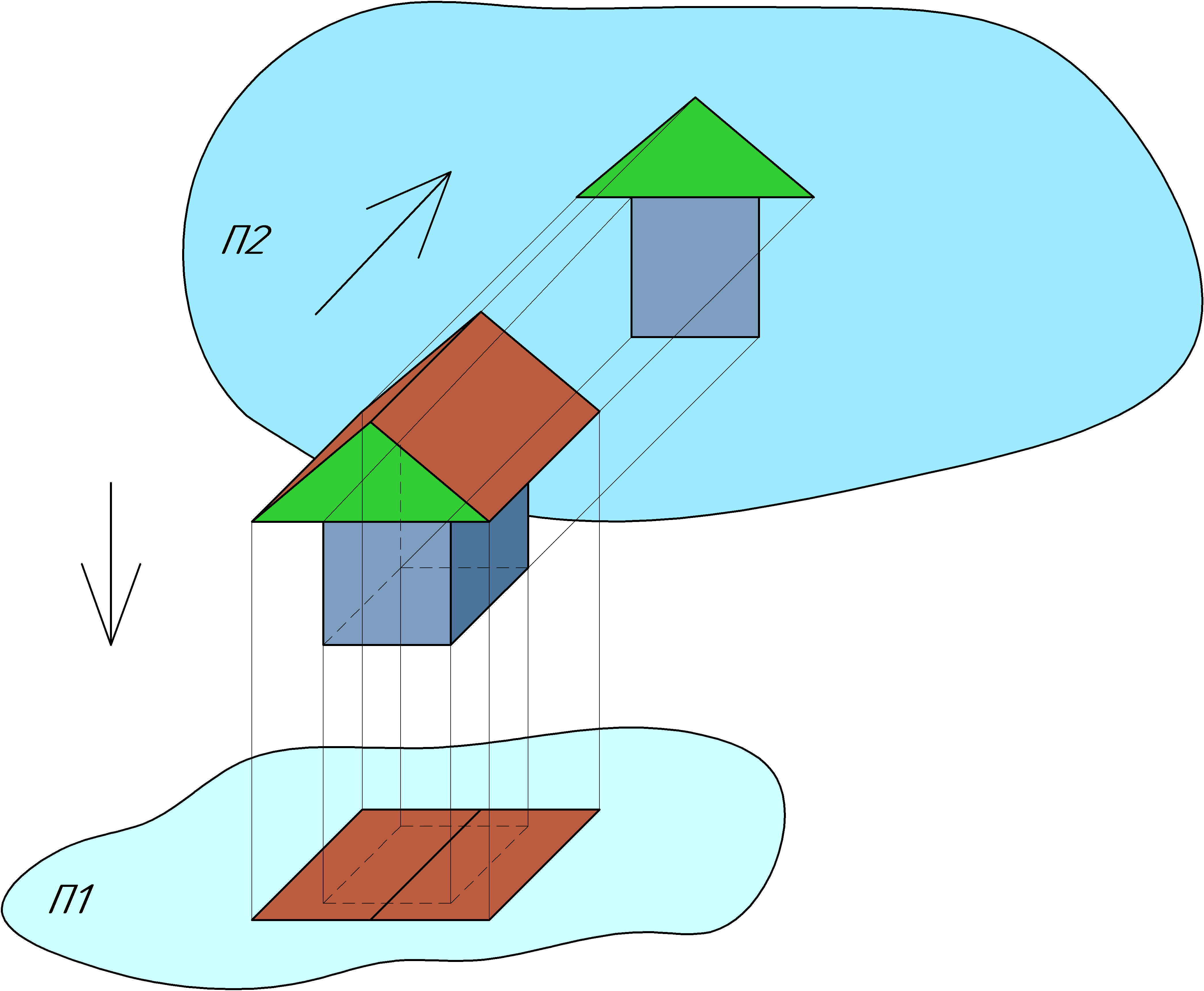 Имея на руках некоторую сложную деталь или предмет, особенно с вырезами, срезами, отверстиями и прочими элементами, достаточно сложно изобразить ее чертеж используя лишь одну плоскость проекций (если только это не сфера, цилиндр или другая простая деталь с несколькими отверстиями). Для этих целей используются несколько плоскостей, видов, разрезов. Вернемся к предыдущему примеру и построим другую проекцию дома. Для этих целей введем еще одну плоскую поверхность (плоскость), которая будет располагаться за домиком. Осветив его с нашей стороны, стороны наблюдателя, на П2 можно будет увидеть второй чертеж дома, фасад. По этому чертежу можно судить о высоте крыши, стен и расположении окон или дверей, если бы они тут были. В некотором плане, уже можно построить дом в совсем упрощенном виде, без всяких дополнительных элементов и деталей. В реальной жизни, в чертежах домов будет множество дверей, окон, перегородок и прочих инженерных сооружений или коммуникаций.
Имея на руках некоторую сложную деталь или предмет, особенно с вырезами, срезами, отверстиями и прочими элементами, достаточно сложно изобразить ее чертеж используя лишь одну плоскость проекций (если только это не сфера, цилиндр или другая простая деталь с несколькими отверстиями). Для этих целей используются несколько плоскостей, видов, разрезов. Вернемся к предыдущему примеру и построим другую проекцию дома. Для этих целей введем еще одну плоскую поверхность (плоскость), которая будет располагаться за домиком. Осветив его с нашей стороны, стороны наблюдателя, на П2 можно будет увидеть второй чертеж дома, фасад. По этому чертежу можно судить о высоте крыши, стен и расположении окон или дверей, если бы они тут были. В некотором плане, уже можно построить дом в совсем упрощенном виде, без всяких дополнительных элементов и деталей. В реальной жизни, в чертежах домов будет множество дверей, окон, перегородок и прочих инженерных сооружений или коммуникаций.
Точка в двух проекциях
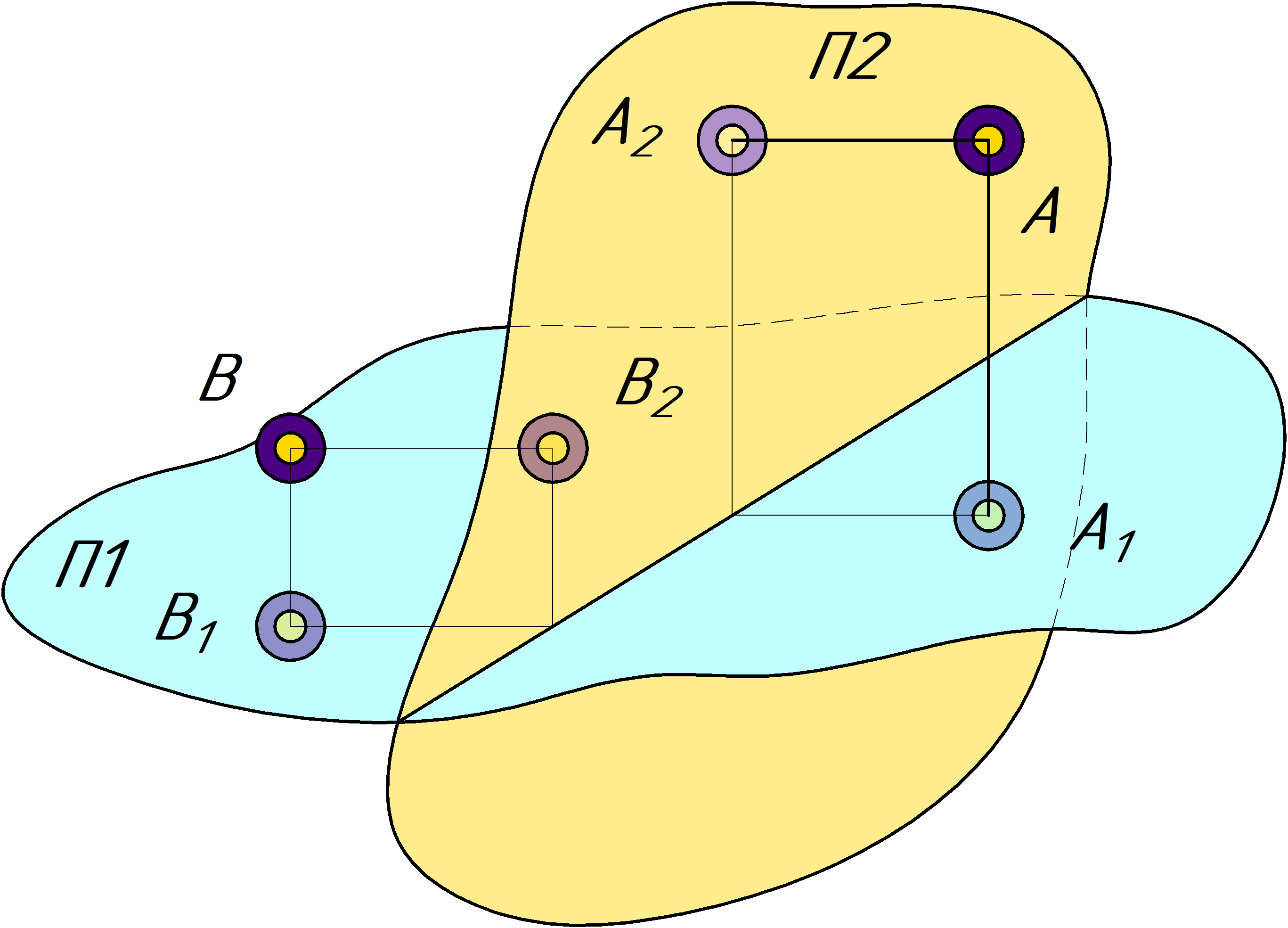 Разобравшись с изображением деталей на чертеже, рассмотрим изображение точек в системе двух плоскостей проекций, после чего построим их чертеж. На рисунке представлены две точки в пространстве, B и A. Стоит отметить, что точки располагаются в разных пространствах и их чертежи будут немного отличаться друг от друга. Цвет точек, которые располагаются в пространстве, показан более темным цветом. Их отображения на плоских поверхностях показаны более тусклым цветом и подписаны соответствующим индексом. Стоит отметить, что в данном случае индекс показывает принадлежность отображения точки той или иной поверхности, а не расстояние в метрах, как в числовых отметках. Имея каждую точку и по два их изображения, построим плоский чертеж.
Разобравшись с изображением деталей на чертеже, рассмотрим изображение точек в системе двух плоскостей проекций, после чего построим их чертеж. На рисунке представлены две точки в пространстве, B и A. Стоит отметить, что точки располагаются в разных пространствах и их чертежи будут немного отличаться друг от друга. Цвет точек, которые располагаются в пространстве, показан более темным цветом. Их отображения на плоских поверхностях показаны более тусклым цветом и подписаны соответствующим индексом. Стоит отметить, что в данном случае индекс показывает принадлежность отображения точки той или иной поверхности, а не расстояние в метрах, как в числовых отметках. Имея каждую точку и по два их изображения, построим плоский чертеж.
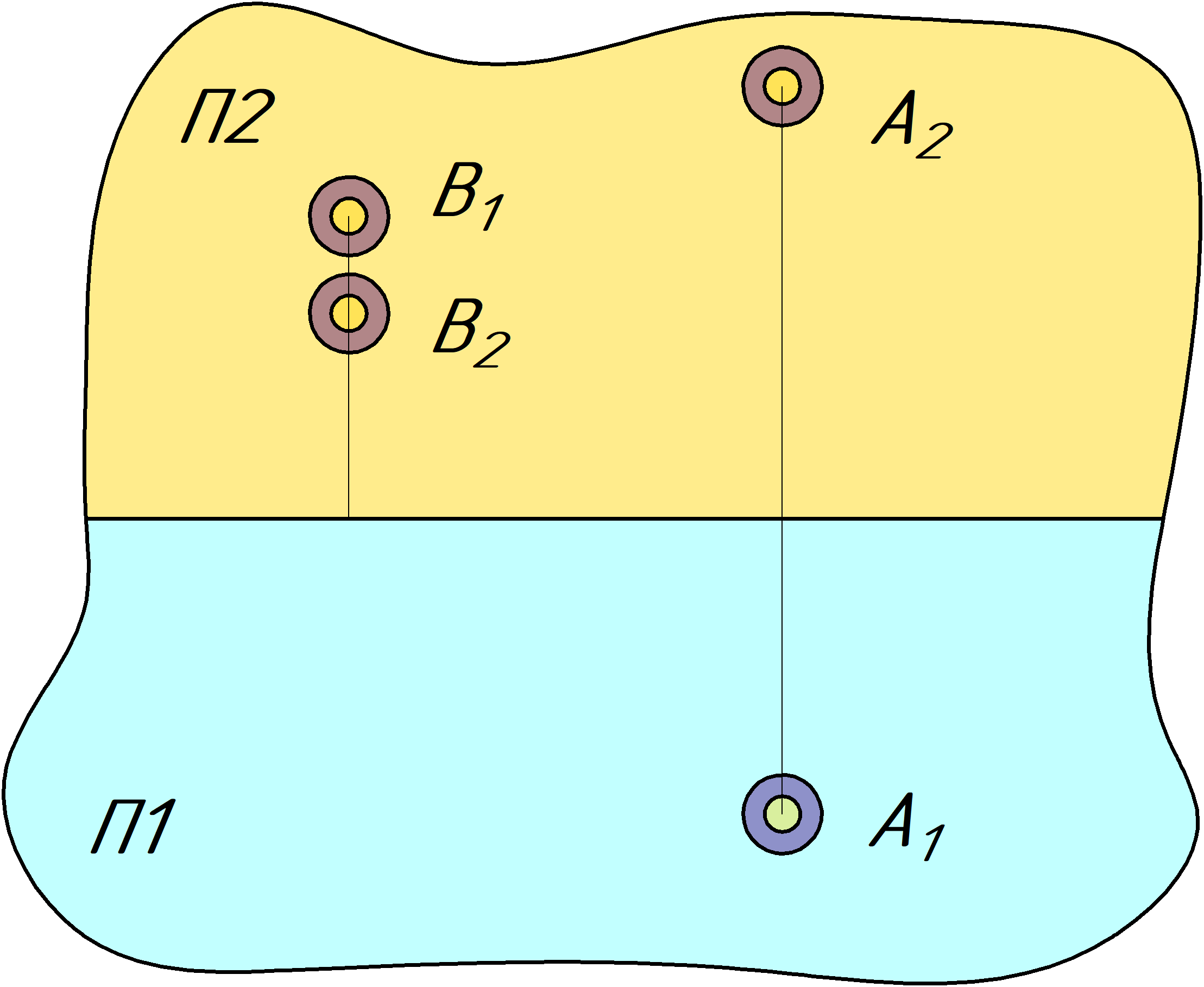 Для получения плоского чертежа две плоскости вращаются вокруг линии их пересечения до соединения. Условно плоскость П1 расположена снизу, а П2 сверху, хотя по сути, эти плоскости простираются
бесконечно в пространстве и "заходят" друг за друга. Расстояние от линии пересечения плоскостей до точки A1 и B1 - это расстояние точки по оси Y. По рисунку и аксонометрии можно отметить что
координатат точки А по Y положительная, а для точки B - отрицательная. Расстоячние от линии пересечения плоскостей до B2 и А2 - это координата по Z. В нашем случае, у обоих точек эта координата
положительная. При построении следует отмечать, какой октант занимает точка по отношению к плоскостям проекций, тогда легче будет построить ее чертеж на плоском листе. А для построения точки в двух проекциях онлайн имеется
инструмент на данной странице. Имея координаты и введя их в окно, после нажатия кнопки "показать", можно получить ее чертеж за доли секунды. На сайте имеется еще один инструмент, который поможет построить точку в трех проекциях онлайн.
Для получения плоского чертежа две плоскости вращаются вокруг линии их пересечения до соединения. Условно плоскость П1 расположена снизу, а П2 сверху, хотя по сути, эти плоскости простираются
бесконечно в пространстве и "заходят" друг за друга. Расстояние от линии пересечения плоскостей до точки A1 и B1 - это расстояние точки по оси Y. По рисунку и аксонометрии можно отметить что
координатат точки А по Y положительная, а для точки B - отрицательная. Расстоячние от линии пересечения плоскостей до B2 и А2 - это координата по Z. В нашем случае, у обоих точек эта координата
положительная. При построении следует отмечать, какой октант занимает точка по отношению к плоскостям проекций, тогда легче будет построить ее чертеж на плоском листе. А для построения точки в двух проекциях онлайн имеется
инструмент на данной странице. Имея координаты и введя их в окно, после нажатия кнопки "показать", можно получить ее чертеж за доли секунды. На сайте имеется еще один инструмент, который поможет построить точку в трех проекциях онлайн.