Построение 3х проекций точки на эпюре Монжа онлайн

Координаты точки А:

Координата по X():

Координата по Y():

Координата по Z():

Деталь на чертеже

Во многих ситуациях чертежа, который состоит из двух видов недостаточно, в таком случае создается ее третья проекция. На рисунке показана деталь, имеющая призматическую голову и цилиндрическое основание. На чертеже, который расположен справа, сложно понять, из какой формы состоит эта деталь. Голова может быть прямоугольной, либо это цилиндр, либо квадрат. По нижней части тоже можно запутаться, вместо цилиндра, это может быть призма и наоборот. Чтобы дать однозначный ответ без всякого рода предположений, делается еще одна, 3я проекция. На чертеже слева это П3. На этом виде уже понятно что в основании окружность (она выделена красным цветом), а верхняя часть является призматической. Таким образом, получается полноценный чертеж детали, которую можно воспроизвести на предприятии-изготовителе. На деле же, многие предметы нас окружающие, состоят из более сложных элементов и кроме трех проекций, для создания их чертежа, потребуются еще несколько дополнительных видов, разрезов или сечений.

Проекция предметов на 3и плоскости проекций

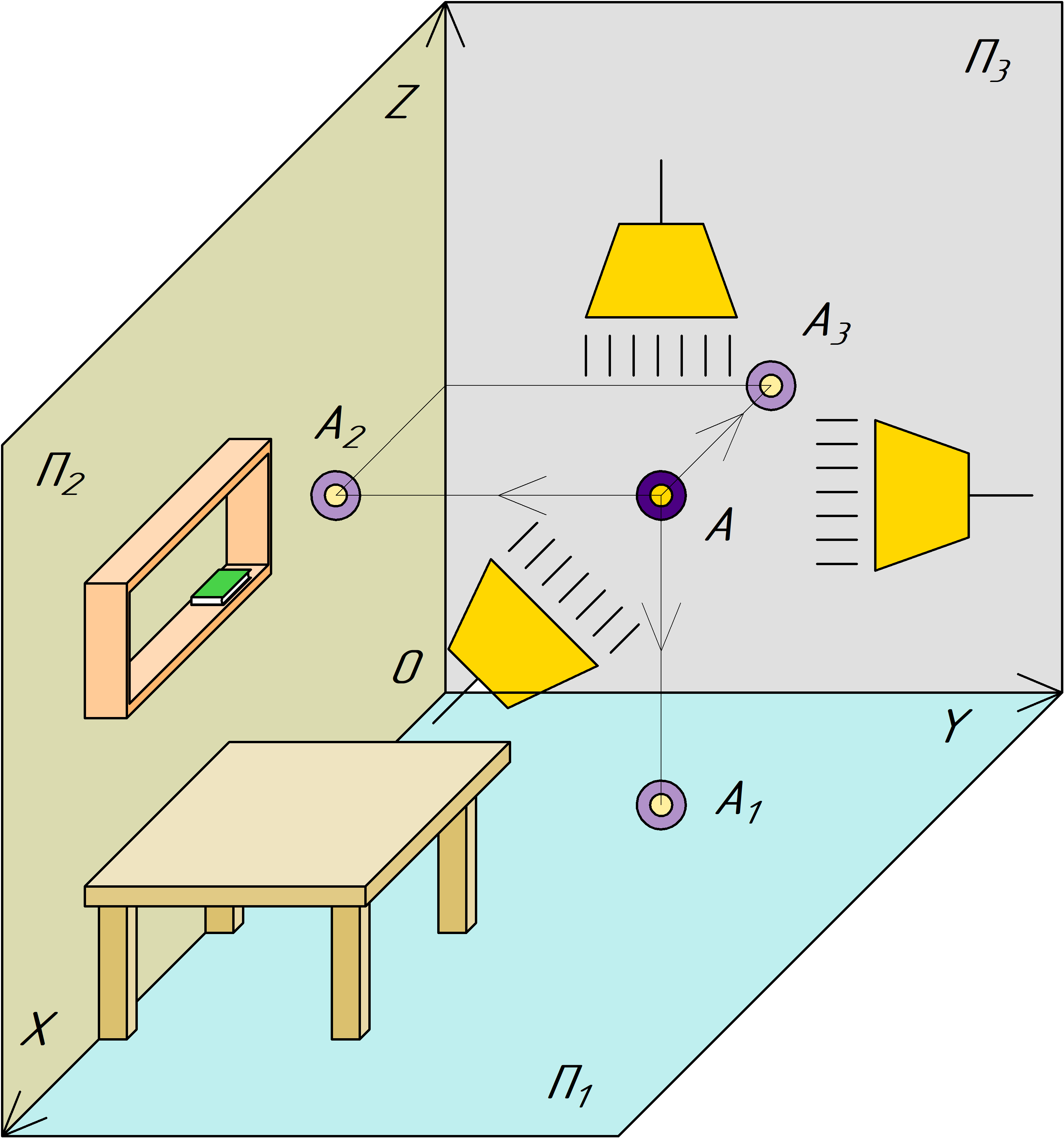Для изучения проекций точки, обратимся к примеру с проецированием предметов. На рисунке представлена импровизированная комната, в которой пол условно представляет собой плоскость П₁, передняя стенка будет представлять плоскость П₂, боковая стенка - П₃. Угол принят за точку отсчета, а места плинтуса используются в качестве осей. В центре комнаты, на некоторой высоте располагается некоторая точка. Имея точку в пространстве, "подсветим" ее равномерными источниками света так, чтобы тени падали перпендикулярно стенкам и полу. В результате получим три тени, другими словами, проекции. Убрав эту точку и оставив проекции, можно решить обратную задачу по нахождению ее положения в пространстве. Приведем пространственный чертеж нашей комнаты к плоскому чертежу и рассмотрим предметы на эпюре Монжа.

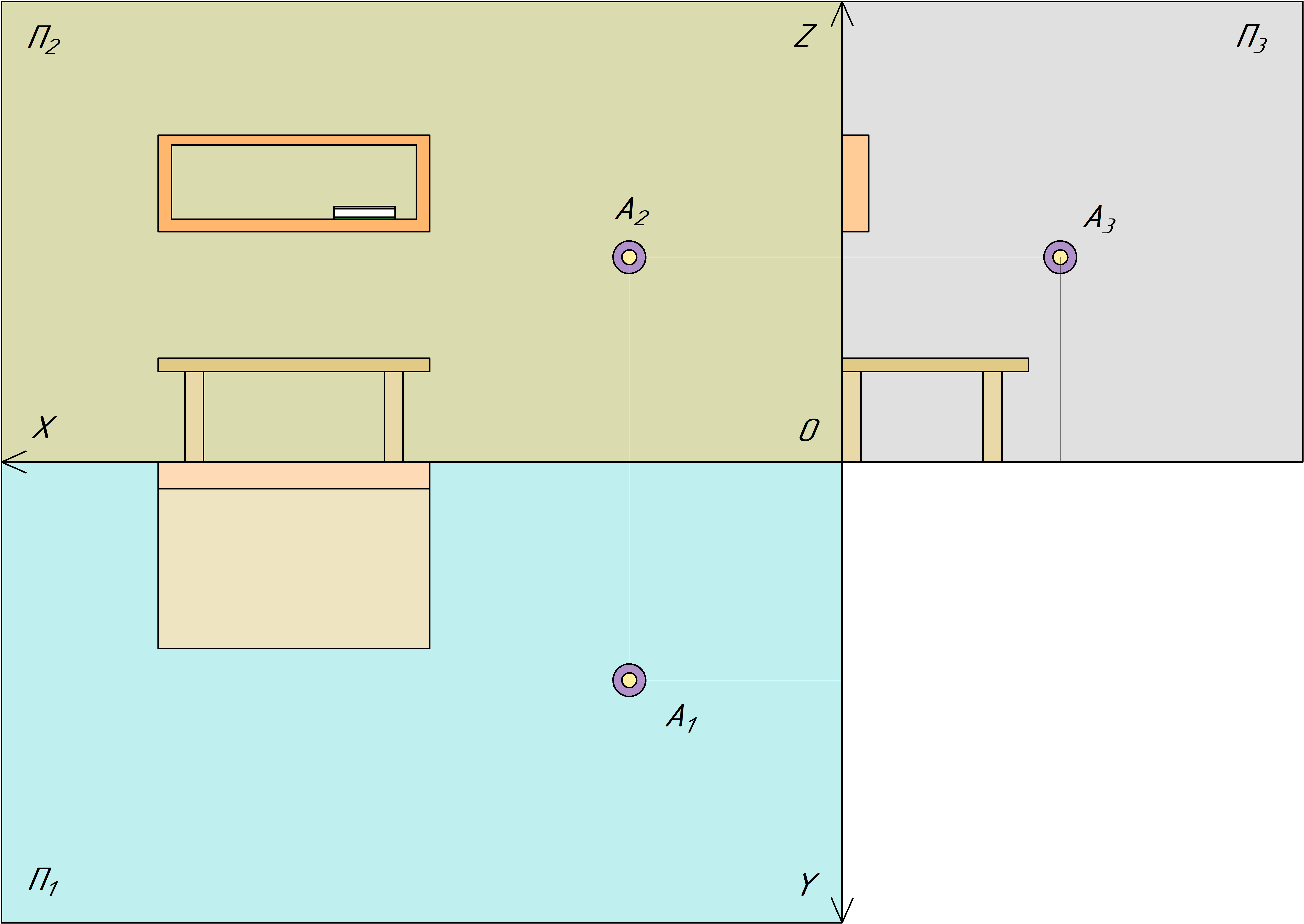Плоский чертеж получается поворотом пола в вертикальное положение и стенки П₃ совпадающей с П₂. Главный вид, П₂, дает нам общее представление о положении стола и полки, форму отверстия полки и ножки у стола, его высота и точку А, ее координаты по Х и по Z. На плоскости П₁ можно увидеть толщину полки, столешницу и определить координаты точки А по Х и по Y. На дополнительной проекции, П₃ показаны уточняющие элементы. К примеру, имея две проекции стола сложно понять, ножки у него сплошной длины или там 4е отдельных стойки, в нашем случае это будут отдельные 4е стойки, о чем и говорит нам 3я проекция. На ней так же можно определить расстояние и просвет между столом и полкой и другие дополнительные элементы. Для точки можно определить координаты по Y и Z. Соединив эти плоскости в обратном направлении, можно получить пространственную картину комнаты, которая показана на рисунке выше.

Онлайн чертеж точки на трехпроекционном эпюре

На данной странице представлен инструмент, помогающий в расстановке трех проекций точки в режиме онлайн. В данном случае речь идет не о математической системе координат, декартовой, а об эпюре Монжа. В математике можно нарисовать точку в пространстве по трем координатам или на плоском листе сделать чертеж точки в системе двух координат. На эпюре Монжа можно выполнить чертеж точки в пространстве, используя метод проекций. Другими словами, имея те же три координаты, можно сделать плоский чертеж точки, показывая их принадлежность той или иной плоской поверхности (они еще называются плоскостями проекций). Суть способа заключается в том, что координатная ось используются несколько раз. Например, для точки с индексом "1" горизонтальная и вертикальные оси будут иметь значения по X и по Y. X влево будет положительная, вправо отрицательная, с осью Y - вниз будут положительные значения, вверх - отрицательные. Для точки с индексом "2" горизонтальные и вертикальные оси будут иметь значения по X и по Z. Для точки c индексом "3" - значения по Y (эта ось уже будет занимать горизонтальное положение) и по Z. Для определения положения проекций, достаточно ввести координаты точек и нажать кнопку "показать". На мольберте будут автоматически начерчены три проекции точек. Стоит отметить, что данный инструмент принимает как положительные значения координат, так и отрицательные. В случае, если требуется найти третью проекцию точки по двум имеющимся, существует на данном сайте другой инструмент, который доступен по ссылке или с главной страницы.

Использование калькулятора

На видео, которое представлено чуть ниже описана работа с калькулятором по отрисовке точек онлайн.

Полезные ссылки

Отрезок AB на двух видах
Решить задачу на построение некоторого отрезка на эпюре Монжа можно используя некоторые правила построения. В случае, если точки имеют отрицательные координаты и расположены в разных четвертях пространства, построение усложняется. Для данных целей и создана эта страница, на которой можно посмотреть на решение данной задачи.

Точка в трех проекциях
В глобальной сети хорошо показаны чертежи точек, отрезков и плоскостей, координаты которых имеют положительные значения. Это и наглядно и просто. Однако как быть, если заданы отрицательные значения у той же точки? В данном случае возникают сложности с построением. На данной странице есть инструмент, который поможет в отрисовке точки на плоском чертеже.

Чертеж шпонки призматической с исполнениями
Для более подробного изучения шпоночного соединения, создания чертежа по индивидуальным размерам и была разработана данная страница. Здесь возможно посмотреть на чертеж шпонки в режиме реального времени, задавая свое параметры данного металлического изделия, ширину, высоту, длину и исполнение. В результате расчета будут построены три проекции шпонки и указаны ее размеры в мм.

Чертеж болтового соединения с расчетом онлайн
На данной странице можно получить чертеж болтового соединения онлайн. Для этого необходимо лишь ввести нужные параметры, наружный диаметр резьбы болта, шаг и толщину соединяемого пакета (пластин А и Б). После ввода и нажатия кнопки "показать" программа построит чертеж онлайн и проведет расчет соединения. Отрисовка будет производиться онлайн при помощи графики HTML.

Получить чертеж муфты короткой онлайн
Чертеж муфты короткой состоит из двух видов, главного и вида слева. Перейдя по этой ссылке и введя параметры, можно получить ее чертеж. Кроме двух видов с размерами, под окном будет указано наименование данного изделия и параметры трубной резьбы. Дополнительно в опциях можно указать масштаб вычерчиваемого изображения.

Чертеж развертки правильной пирамиды онлайн
Многие задачи в черчении требуют построения развертки той или иной поверхности. Для облегчения этой задачи была создана данная страница, расположенная по ссылке. Здесь можно построить чертеж боковой поверхности правильной пирамиды, введя всего лишь 4е параметра. Отрисовка будет произведена автоматически за несколько секунд.

Отображение размеров развертки цилиндра онлайн
Развертка поверхности цилиндра представляет собой прямоугольник и две окружности. Введя данные высоты и диаметров оснований, на этой странице можно получить финальный чертеж этой поверхности как если бы ее делали на плоском листе бумаги. Стоит оговориться, что в результате будет получен чистый чертеж поверхности без полосок для соединения или склеивания поверхности.

Плоскость на эпюре на горизонтали и фронтали
В интернете хорошо описаны решения задач, когда точки или плоскости располагаются в 1й четверти пространства. Однако как быть, если точки плоскости имеют отрицательные значения и расположены за пределами нужного октанта? Данный инструмент поможет в этом. Единственно, координаты по оси ОХ должны быть положительными, так как в данном случае используются всего лишь две проекции.