Задачи на нахождение элементов на расстоянии
 В начертательной геометрии существуют задачи, в которых необходимо найти элементы на некотором расстоянии от плоскости проекций, П1, П2, П3 или от других каких-нибудт плоскостей/прямых/точек.
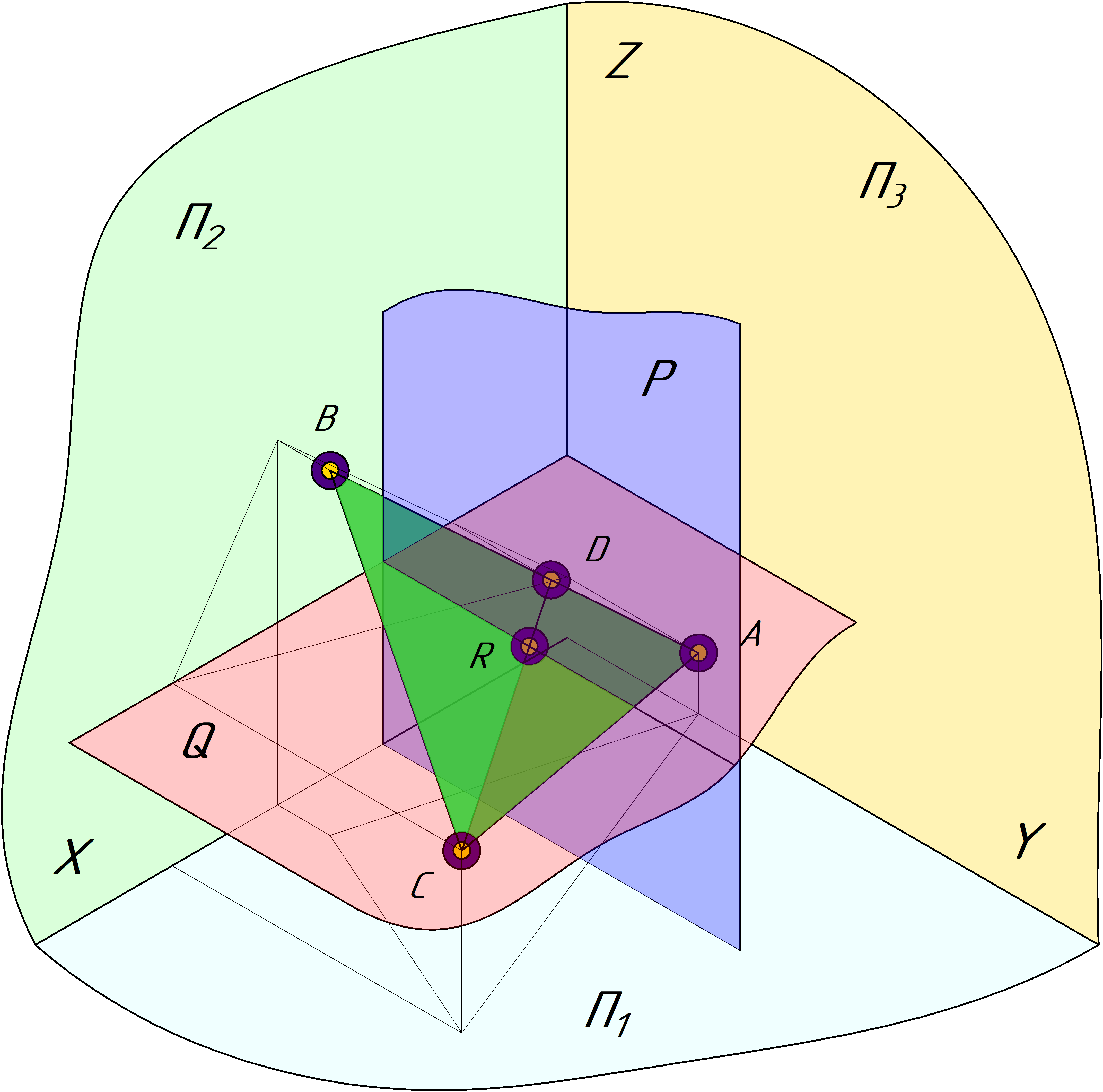
Данный тип задач, в основном, решается с применением вспомогательных плоскостей. Рассмотрим некоторую задачу, где дана плоскость и требуется найти точку на некотором расстоянии от П1 и П3. Для упрощения
задачи, координаты точек указывать не будем, как и расстояния до плоскостей, рассмотрим суть решения. Для начала, представим что из себя будет представлять плоскость ABC и плоскость Q, которая параллельна плоскости
П1. Это будет некоторая общая прямая линия, в данном случае проведенная из точки С и параллельная плоскости П1, ее еще называют "горизонталь" (CD). Для решения остается лишь найти точку ее пересечения
с плоскостью P, которая параллельна П3 и расположенная от нее на некотором расстоянии. В результате получим точку R как результирующую. Таким же образом можно найти и третью проекцию точки по двум имеющимся.
В начертательной геометрии существуют задачи, в которых необходимо найти элементы на некотором расстоянии от плоскости проекций, П1, П2, П3 или от других каких-нибудт плоскостей/прямых/точек.
Данный тип задач, в основном, решается с применением вспомогательных плоскостей. Рассмотрим некоторую задачу, где дана плоскость и требуется найти точку на некотором расстоянии от П1 и П3. Для упрощения
задачи, координаты точек указывать не будем, как и расстояния до плоскостей, рассмотрим суть решения. Для начала, представим что из себя будет представлять плоскость ABC и плоскость Q, которая параллельна плоскости
П1. Это будет некоторая общая прямая линия, в данном случае проведенная из точки С и параллельная плоскости П1, ее еще называют "горизонталь" (CD). Для решения остается лишь найти точку ее пересечения
с плоскостью P, которая параллельна П3 и расположенная от нее на некотором расстоянии. В результате получим точку R как результирующую. Таким же образом можно найти и третью проекцию точки по двум имеющимся.
Третья проекция точки по двум имеющимся
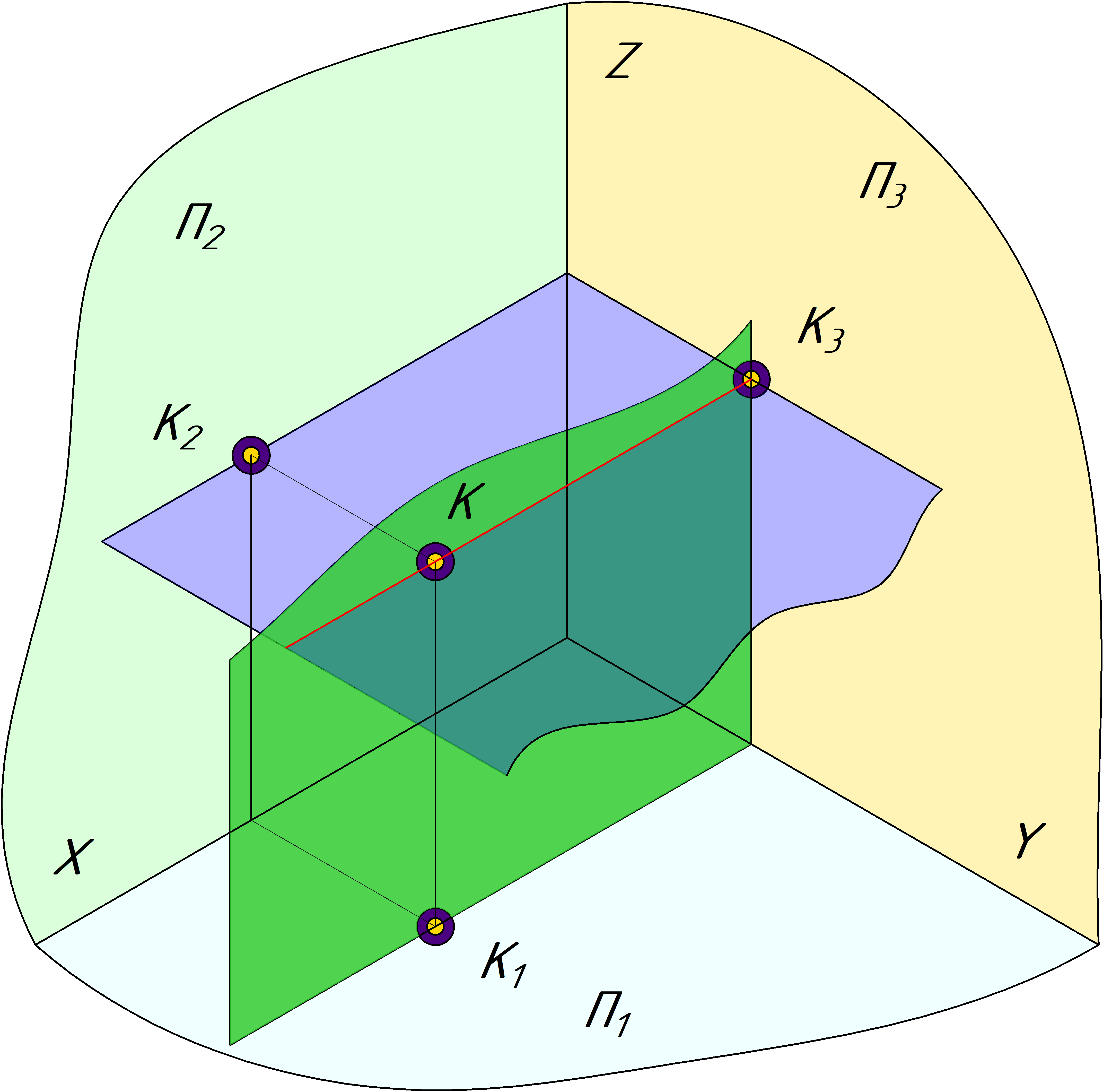 Одной из таких задач является и задача на нахождение некоторой неизвестной проекции точки. Ее так же можно решить, используя некоторые вспомогательные плоскости. В данном случае имеется некоторая точка К и ее две проекции
на П1 и П2. Проведя две плоскости через точку, на П3 в месте их пересечения будет точка, являющаяся ее 3й проекцией. В данном случае были проведеняы две плоскости, параллельные горизонтальной
и фронтальной плоскости, профильная плоскость (параллельная П3) в данном случае не дала бы ничего, так как отсекаемые линии уже содержат проекции точки К. Данную задачу можно решить и другим способом.
К примеру, имея две проекции, как в нашем случае, у точки К уже имеются все 3и координаты, по X, Y, Z. Остается отметить эти координаты (по Y и Z) на 3й плоскости проекций, после чего отметить точку.
Одной из таких задач является и задача на нахождение некоторой неизвестной проекции точки. Ее так же можно решить, используя некоторые вспомогательные плоскости. В данном случае имеется некоторая точка К и ее две проекции
на П1 и П2. Проведя две плоскости через точку, на П3 в месте их пересечения будет точка, являющаяся ее 3й проекцией. В данном случае были проведеняы две плоскости, параллельные горизонтальной
и фронтальной плоскости, профильная плоскость (параллельная П3) в данном случае не дала бы ничего, так как отсекаемые линии уже содержат проекции точки К. Данную задачу можно решить и другим способом.
К примеру, имея две проекции, как в нашем случае, у точки К уже имеются все 3и координаты, по X, Y, Z. Остается отметить эти координаты (по Y и Z) на 3й плоскости проекций, после чего отметить точку.
Проекция точки онлайн с координатами
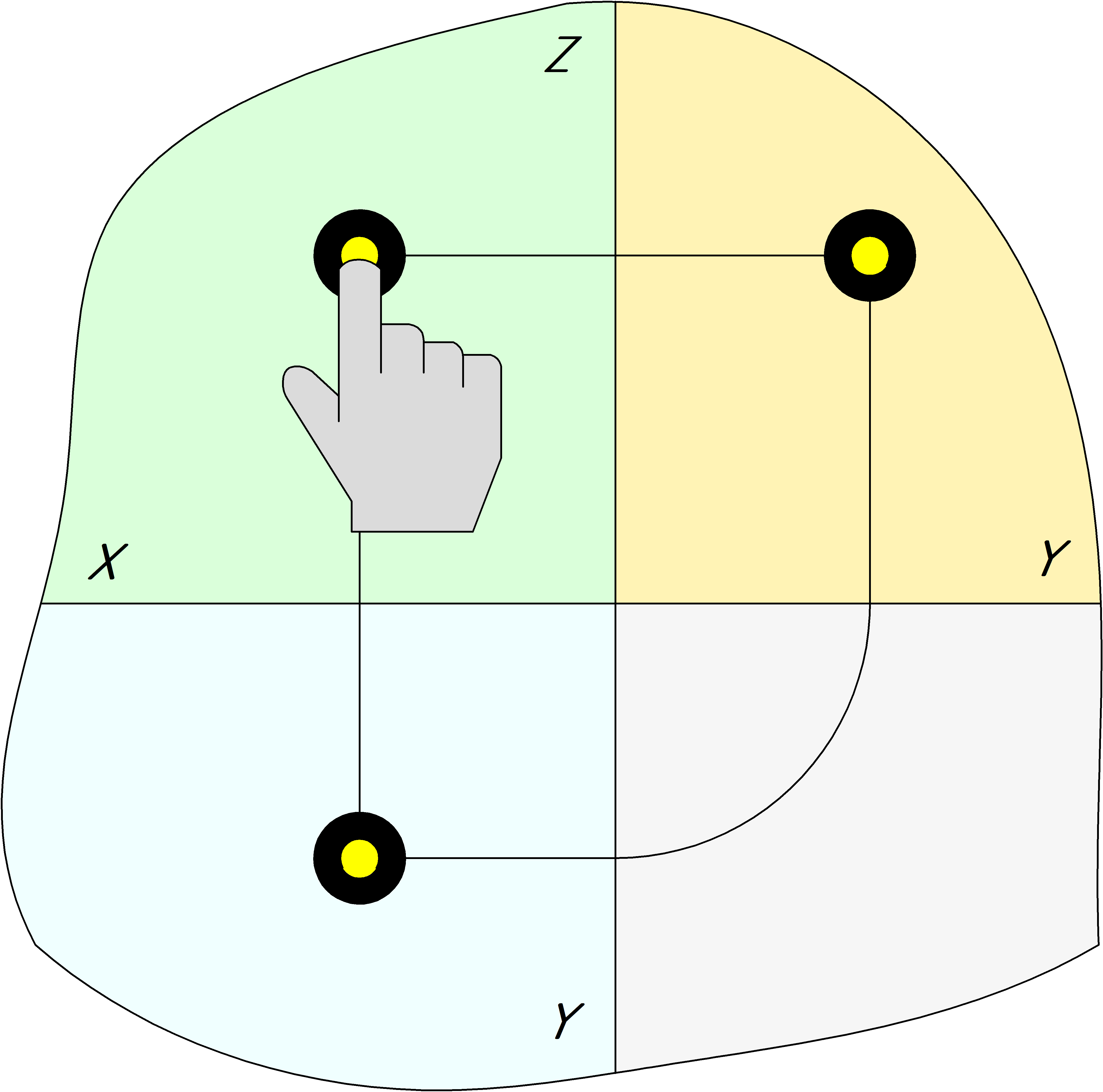 По данному принципу определения координаты точки и построен данный калькулятор. На этой странице можно разместить проекции точки, после чего получить ее координаты нажав кнопку "показать", либо найти расположение третьей проекции
онлайн. Определение координат точек достаточно простое дело, если точка расположена в 1м октанте и все координаты по осям положительные. Сложности появляются, если точка будет расположена в других октантах, либо если
даны проекции точек на П3 или на П2, либо на осях координат. Данный калькулятор сможет решить такую задачу. Для определения октанта точки онлайн на этой страинце имеется отдельный дополнительный инструмент.
По данному принципу определения координаты точки и построен данный калькулятор. На этой странице можно разместить проекции точки, после чего получить ее координаты нажав кнопку "показать", либо найти расположение третьей проекции
онлайн. Определение координат точек достаточно простое дело, если точка расположена в 1м октанте и все координаты по осям положительные. Сложности появляются, если точка будет расположена в других октантах, либо если
даны проекции точек на П3 или на П2, либо на осях координат. Данный калькулятор сможет решить такую задачу. Для определения октанта точки онлайн на этой страинце имеется отдельный дополнительный инструмент.